A research team from CSIRO Data61 and the Australian Plant Phenomics Facility (APPF) have derived a method for obtaining D-optimal designs for temporal data by proposing incorporating the curvature (or second derivative/acceleration) of the curve as the prior information for optimisation.
“Our team considered the design problem of collecting temporal/longitudinal data,” explained lead author, Dr Jiali Wang.
“In biological and agricultural studies, researchers often monitor the growth of plants, for example, responses to stress conditions over time and different growing trajectories with different genotypes.
“Even with modern high-throughput automatic scanning platforms, cost and time constraints may still make collecting high-frequency data from a large number of biological replicates unrealistic or costly.
“As a consequence, maximising the information gain from limited data and reducing bias when making an inference requires principled guidance,” she added.
“Put simply,” explains APPF Biostatistician, Dr Nathaniel Jewell, “when laboratory or field studies focus on behaviour over time t or some covariate x, two important design questions are then ‘At what values of t or x should measurements be taken?’ and ‘What statistical model should be fitted to the resulting data?’”
Dr Xavier Sirault, Director of the APPF’s CSIRO based node, was a member of the team who developed the new approach.
“When spline models are robust, they typically require a large number of data points.
“However, when past experience, or prior knowledge is available, a smaller and smarter choice of measurement points may be feasible,” he explained.
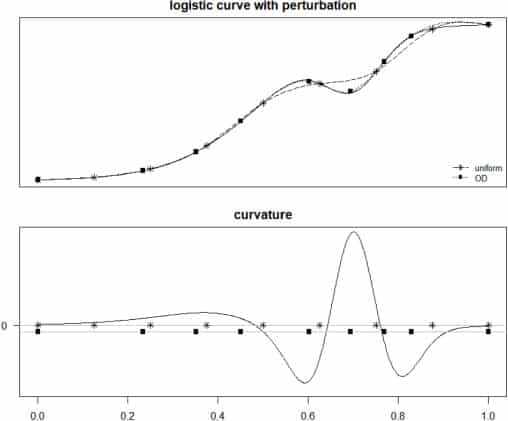
“The prior curvature knowledge is particularly informative when determining optimal sampling points for longitudinal data, because intuitively more observations should be placed at the locations where the shape of the curve is changing rapidly,” said Dr Sirault.
“To the best of our knowledge, including curvature as the prior information in a smoothing spline optimal design problem has not been explored in literature.”
In the paper, the adaptive smoothing spline is used as the analysis model where the prior curvature information can be naturally incorporated as a weighted smoothness penalty. The estimator of the curve is expressed in linear mixed model form, and the information matrix of the parameters is derived. The D-optimality criterion is then used to compute the optimal design points. An extension is considered, for the case where sub-populations exert different prior curvature patterns.
“We compare properties of the optimal designs with the uniform design using simulated data and apply our method to the Berkeley growth data to estimate the optimal ages to measure heights for males and females”, explained Dr Wang.
“The approach is implemented in an R package called “ODsplines”.
“Dr Wang et al have written an R package to choose measurement points intelligently, and have shown that the method performs well under spline-based regression,” said Dr Jewell.
The R package called “ODsplines”, is available from GitHub here.
Read the paper “Optimal design for adaptive smoothing splines”.